소프트웨어 개발 현장에서의 수학
수학 개념 및 수학적 접근법을 통해 소프트웨어 개발 현장에서 겪는 복잡한 문제를 단순한 형태로 모델링할 수 있다.
마이그레이션의 부분 순서 모델
문제 상황은 SemVer를 따르는 라이브러리의 메이저 버전을 위해 마이그레이션을 지원하는 것이다. 각 메이저 버전에는 이전 버전의 코드를 자동으로 변환해주는 변환기가 함께 배포된다. 만약 1.x에서 3.x로 업데이트할 때는 2.x 변환기, 3.x 변환기를 순차적으로 실행해야 한다. 즉, 하위 버전에서 출발해 상위 버전에 도착하는 경로를 구해야 한다.
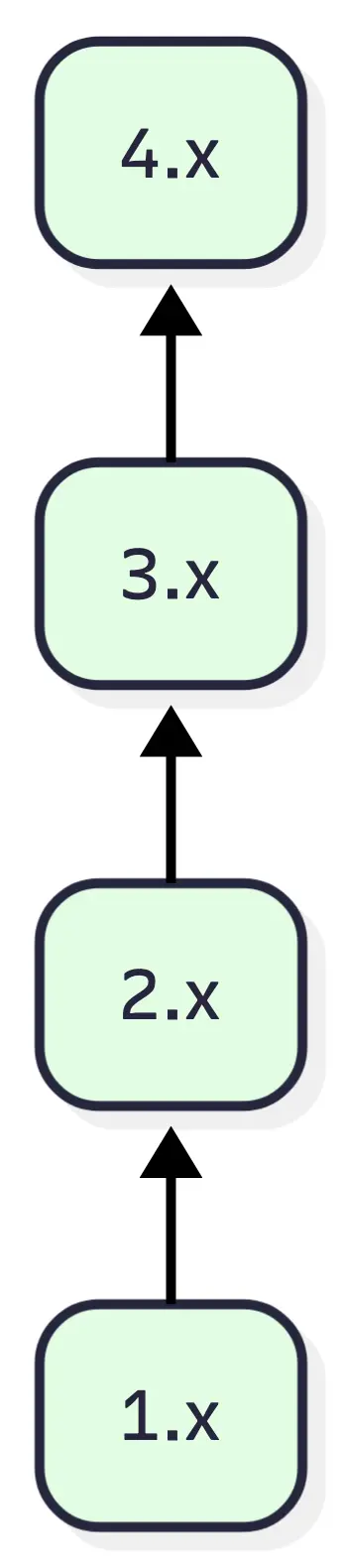안정 버전만 고려한 순서.
그런데 베타 버전(x.y-beta)과 알파 버전(x.y-alpha.z)을 고려해야 한다. 베타 버전에는 직전 버전에 대한 변환기가 있고, 알파 버전에는 변환기가 없다. 나이브하게 생각해보면 출발 버전 유형과 도착 버전 유형의 조합에 대해 모든 경우를 분기해서 경로를 구할 수 있을 것처럼 보인다.
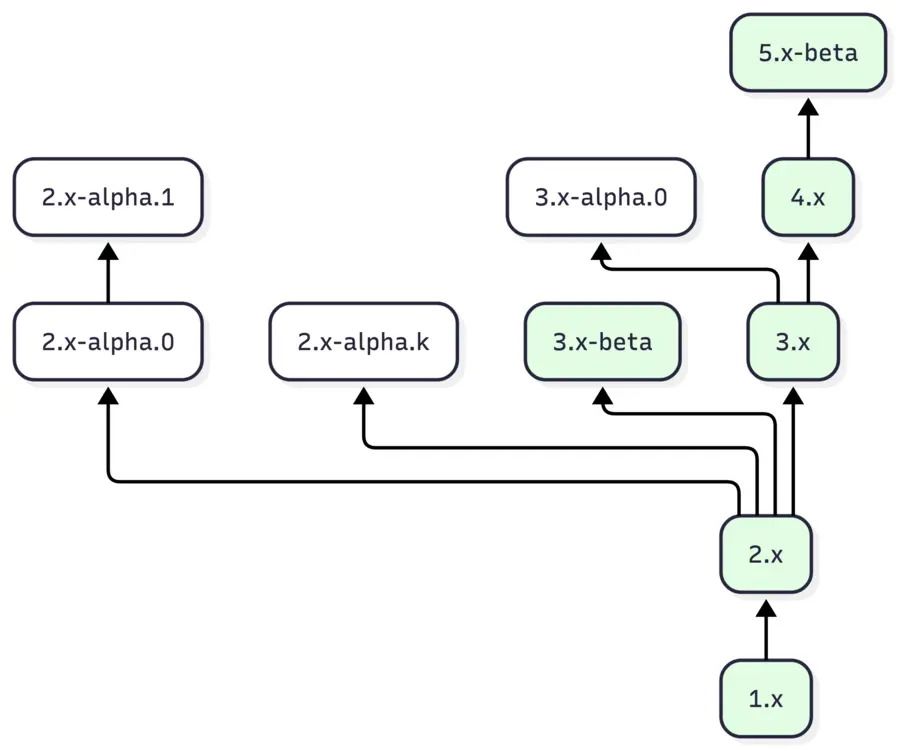베타 버전과 알파 버전까지 고려한 순서.
이를 실제로 조건 분기로 구현해보면 상당히 복잡해진다. 더 일반화된 방법이 필요하다. 버전 관계를 다시 정의해보자. 변환기를 기준으로 생각해보면 모든 버전 사이에 순서가 있다고 할 수는 없다. 버전을 poset으로 모델링해보면 어떨까? a
(1.x, 3.x)는 모든 조건을 만족하기 때문에 변환기를 거쳐 마이그레이션할 수 있다. (1.x, 3.x-beta)도 모든 조건을 만족한다. 반면 (3.x-beta, 1.x)는 (1), (3)을 위반하기 때문에 변환기를 사용할 수 없다. (2.x-alpha.1, 3.x-alpha.0)는 (1), (2)를 위반한다. 이렇게 출발 버전부터 시작해 a
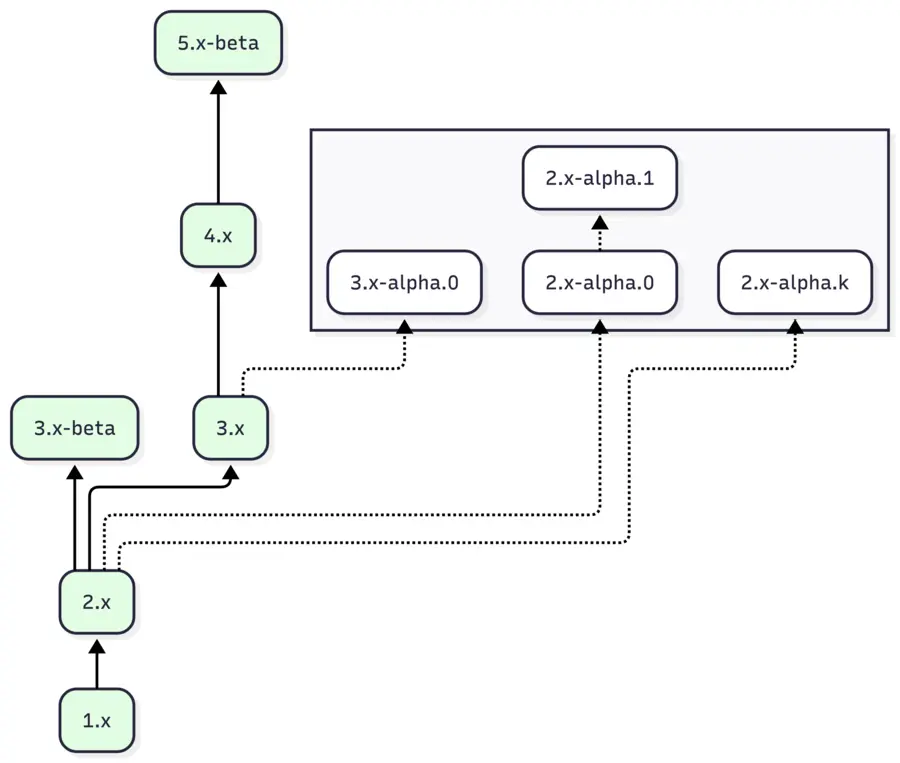마이그레이션이 가능한 관계와 불가능한 관계.