A* 탐색

Pseudo Code
휴리스틱 함수
예시
- 미로 찾기
- 8 퍼즐
Evaluation
참고자료
이 문서를 인용한 문서

BFS 기반의 그리디한 해 탐색 알고리즘.
- BFS는 최적해를 찾기는 하지만 탐색 순서를 지능적으로 결정하지 않기 때문에 많은 노드를 탐색해야 함.
- A* 탐색은 휴리스틱 함수로 현재 위치에서 도착점까지의 예상 길이를 계산하고, 가장 짧은 경로를 먼저 탐색한다.
- 휴리스틱 함수를 사용하는 개선된 다익스트라 알고리즘으로 이해할 수도.
A* 탐색으로 풀 수 있는 문제는 가장 짧은 depth에 있는 solution leaf를 찾는 문제:
- 미로 찾기: 시작점부터 가장 빨리 탈출할 수 있는 경로 찾기.
- 내비게이션: 시작점부터 가장 빨리 목적지에 도착할 수 있는 경로 찾기.
- 8퍼즐: 최소한의 이동으로 퍼즐을 완성하기.
스타크래프트 등 각종 게임과 내비게이션에 사용, HPA*, IDA*, D* 등 다양한 변형이 존재.

Pseudo Code

루트부터 시작하여, 루트의 $\hat f(x)$ 를 계산하고 open(priority queue)에 추가한다.
open에서 $\hat f(x)$ 가 가장 작은 노드를 꺼내 closed(set)에 추가한다.
해당 노드와 연결된 노드들의 $\hat f(x)$ 를 계산한다.
연결된 노드가 open에 있고, 기존 경로보다 빠르게 도착했다면: $\hat f(x)$ 를 갱신한다.
연결된 노드가 closed에 있고, 기존 경로보다 빠르게 도착했다면: $\hat f(x)$ 를 갱신하고, closed에서 제거한 뒤 open에 추가한다.
연결된 노드가 open이나 closed에 없다면: open에 추가한다.
연결된 노드 중 하나가 도착점이면 종료한다. 아니라면 2번으로 돌아간다.

open = PriorityQueue()
open.put(start)
closed = set()

while open:
    now = open.pop()

    if now == goal:
        break
    closed.add(now)

    for next in neighbors(now):
        cost = now.g + w(now, next)

        if next in open and next.g <= cost:
            continue
        elif next in closed:
            if next.g <= cost:
                continue
            closed.remove(next)
            open.put(next)
        else:
            next.h = h(next, goal)
            open.put(next)
        next.g = cost

휴리스틱 함수

\hat f(x) = \hat g(x) + \hat h(x)

노드의 '좋은 정도’를 평가:
- $\hat g(x)$ : 시작점부터 노드 $x$ 까지의 최단 경로 길이 추정. (현재까지 탐색한 최단 경로 길이)
- $\hat h(x)$ : 노드 $x$ 부터 도착점까지의 최단 경로 길이 추정. (휴리스틱 함수)
- $\hat f(x)$ : 시작점부터 노드 $x$ 를 지나 도착점까지의 최단 경로 길이 추정.
휴리스틱(Heuristic): 불충분한 정보로 판단이 어려울 때 선험적인 지식을 기반으로 추론하는 방법.
휴리스틱 함수에 따라 A* 탐색은 최적해를 보장하지 않을 수 있다.
- 탐색 도중 도착점에 도달하는 순간 중단하기 때문.
- 따라서 도착점에 도달하기 전에 ‘좋아 보이는’ 경로를 모두 탐색해야 한다.
- 어떤 경로가 좋아 보이는지 판단하기 위해 휴리스틱 함수를 사용한다.
휴리스틱 함수는 실제 경로의 길이보다 작거나 같은 값을 가져야 한다. (admissible heuristic function)
- 즉, 예상 길이를 과장하지 않아야 한다.
- depth가 깊은 노드가 아니라 얕은 노드의 $\hat f(x)$ 가 더 작을 수 있기 때문.
- $\hat h(x)$ 가 실제( $h(x)$ )보다 과장되면 depth가 얕은 노드가 선택되지 않을 수 있음.
- 휴리스틱 함수가 admissible하다면 A* 탐색은 최적해를 보장한다.
A* 탐색의 장점을 살리기 위해서는 휴리스틱 함수가 너무 작거나 고른 값이어도 안 된다.
- $\hat h(x) = 0$ 이면 모든 노드의 $\hat f(x)$ 가 시작점으로부터의 거리가 되므로, BFS와 같아진다.
따라서 휴리스틱 함수가 다음 조건을 만족해야 최적해를 보장한다: $0 \leq \hat h(x) \leq h(x)$

예시

미로 찾기

미로에서는 상하좌우로만 이동할 수 있고, 벽을 뚫을 수 없음. 최단 경로로 도착점에 도달해야 한다.
잘 알려진 admissible 휴리스틱 함수는 manhattan distance function.
- 2차원 평면에서 두 정점 $(x_1, y_1)$ 과 $(x_2, y_2)$ 사이의 맨해튼 거리는 $|x_1 - x_2| + |y_1 - y_2|$ .
- 벽을 고려하지 않으므로 실제 거리보다는 작거나 같은 값을 가진다.

8 퍼즐

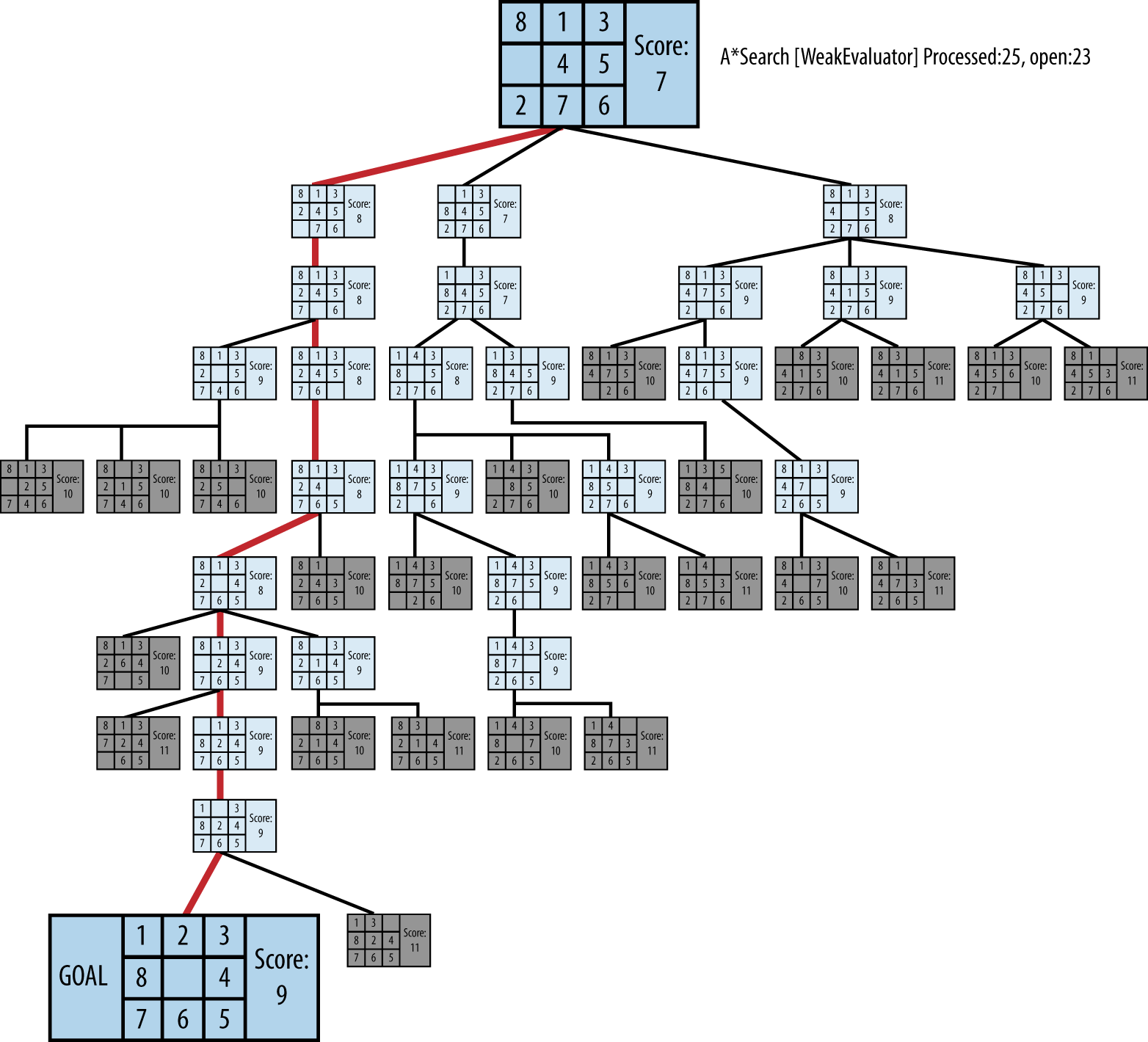
타일을 움직여서 숫자를 정렬하는 퍼즐.
휴리스틱 함수는 제자리에 있지 않은 타일의 수. (현재 게임판의 총 점수)

Evaluation

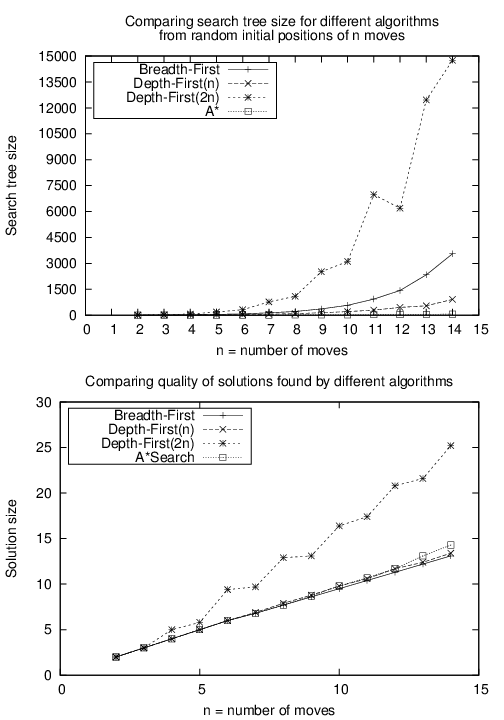
결국 $\hat h(x)$ 가 A* 탐색의 시간복잡도를 결정한다.
최악의 경우 $O(b^d)$ . $d$ 는 해까지의 최단 거리, $b$ 는 트리의 평균 분기율.
$|h(x) - \hat h(x)| \leq \log \hat h(x)$ 이면 $O(d)$ .

참고자료

이 문서를 인용한 문서

알고리즘 및 자료구조